Catenoid Soap Films
The soap film that forms between two parallel circular rings has the
shape of a catenoid, which has the equation r = cosh(z) in cylindrical
coordinates. For a separation/diameter ratio under 0.66274, there
are a thick-necked stable catenoid and a thin-necked unstable catenoid.
At the critical ratio, there is one unstable catenoid. Above the critical
ratio, there are no catenoids.
The images here were made with my
Surface Evolver
program. Click on the small images to get larger versions.
The corresponding datafiles (extension .fe) may be downloaded
by clicking on the links in parentheses.
Stable catenoid (cat.fe)
If the rings are pulled further apart, the neck will narrow until the
critical separation is reached, and then the catenoid will pop into two
disks. Note that the surface becomes unstable before the neck reaches
zero radius.
The unstable catenoid on the same rings as above. For separation/diameter
ratio above 0.4717945, the unstable catenoid can be stabilized by
adding a volume constraint. For a catenoid, the desired volume can
easily be calculated, but one could also adjust the volume until
the pressure is zero. By adjusting the volume so the pressure is
positive or negative, one gets the surfaces known as unduloids and
nodoids, respectively.
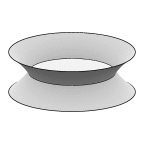
Catenoid with disk (catdisk.fe)
Here the film consists of two sections of catenoid and a flat disk
meeting at 120 degrees. Again, for a separation/diameter ratio below
a critical value, there are a stable thick-necked film and an unstable
thin-necked film. As the rings are pulled apart, the film becomes
unstable before the central disk radius reaches zero.
The wire boundary consists of two pairs of catenoid rings with gaps
joined at right angles. The diagonal lines joining the angle vertices
are lines of 180 degree rotational symmetry. There is a mathematical
theorem that the tangent plane of the film at a corner must be the
tangent plane of the corner. Usually the film is on the inside of the
corner. Only in unusual cases (like the symmetry here) is the film
on the exterior.
Double catenoid with disk (cat1disk.fe)
Having a disk across one of the catenoids spoils the symmetry around
the diagonals, the film becomes tangent to the insides of the angles, although
that level of detail is far too small to be seen in this image.
A close-up of a corner of the double catenoid with one disk. This image
is magnified several hundred times; the lengths of the edges around the
vertex is about 0.0006.
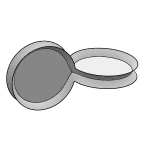
Double catenoid with two disks (cat2disk.fe)
With two disks, the symmetry is restored, and the film is tangent on the
exteriors of the angles. Note that the triple lines meet at a tetrahedral
point singularity where the diagonals cross.
Return to Evolver examples.
Return to Ken Brakke's
home page.
