Surface Evolver Examples
These are some examples of
Surface Evolver surfaces. Some refer to separate pages, others
are self-contained. The datafiles (*.fe) are in DOS text
format (CR-NL end-of-line). Each datafile has comments in it, plus
a typical evolution, usually in the form of a command "gogo".
The first image in each self-contained example is of the surface as defined
in the datafile, before evolution. The other images are evolved.
The evolution generally is not carried to a high refinement, in order
to give reasonable size facets for the images shown.
Click on the small images to get larger images.
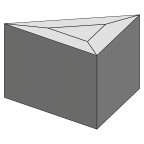
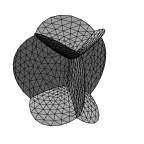Five bubbles, three in a ring around two. The initial
inner film between the two axial bubbles shrinks to a point, and the
resulting vertex needs to be popped. The evolved images show the outer films
and the films between the bubbles respectively.
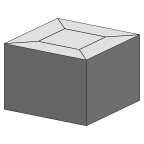
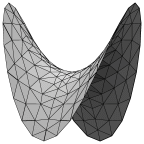
Six bubbles, four in a ring around two.
The central film shrinks here, but unlike 3.fe, it does
not collapse to a point.
The evolved images show the outer films
and the films between the bubbles respectively.
2D surface in 4D. Complex surface w = z^2 defined by constraints.
No evolution, just surface display. Just refine, equiangulate, and admire.
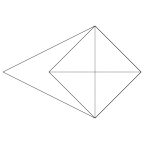
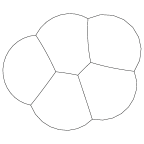A cluster of 5 2-dimensional bubbles. Illustrates string model,
fixed area facets, and vertex popping.
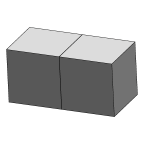
A double bubble, starting as two cubes with a common face. Illustrates
multiple bodies.
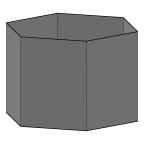
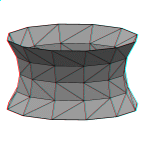A catenoid, which is the soap film formed on two parallel rings.
Illustrates parameterized boundaries, energy saddle points,
tiny edge deletion, and vertex popping. For more catenoids, see
the catenoid soap film page.
A liquid drop between a flat circular pad (green) and a sphere (red).
The volume and contact energy under the sphere are represented by line
integrals around the contact line on the sphere. For explicit contact
facets on the sphere, see
cbga2.fe
Soap films in the form of cones. There are eight of these fitting the
equilibrium rules, but only one turns out to be stable. Illustrates
vertex popping, which knows how to turn unstable vertices like these
cones into combinations of stable tetrahedral vertices.
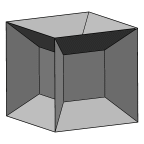
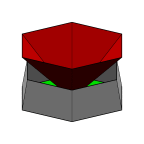
A bubble inside a cubical frame. Illustrates volume constraint, fixed vertices
and edges.
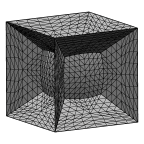
A unit cube evolving into a sphere. Illustrates volume constraint.
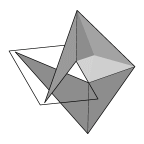
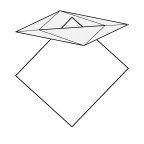
The Hildebrandt-Nitsche cusp formed by a soap film whose boundary is
a skewed spiral looping around the edge of a half-plane. The cusp is
not actually a sharp cusp. The contact lines on the plane curve around
to be tangent to the edge of the half-plane, and the points of tangency
are separated by a short interval (about 0.0175 here) during which the
tangent plane of the film rotates 180 degrees. A magnification of the
cusp is shown in the last image.
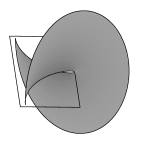
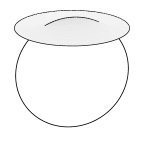Soap film spanning one circle, with another circle poking through the first
to act as a 1-dimensional barrier. The angle between the films on the barrier
wire here is always over 120 degrees, and increases to 180 degrees where the
film leaves the barrier. If the barrier penetrates too far, a stretch of triple
line would form in the interior of the film, and there would be a single film
on the barrier wire between junctions with the triple line.
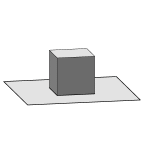
A droplet on a plane surface with gravity and surface contact energy.
Illustrates volume constraint, level-set constraint, using Green's
Theorem to represent contact energy, and the no_refine attribute.
The center surface has no gravity and a 90 degree contact angle. The
right surface has gravity 5 (in dimensionless units)
and a 135 degree internal contact angle.
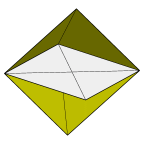
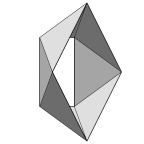
An octahedral frame bounds five stable films and several unstable films.
These are minimal surfaces (in the sense of zero mean curvature)
that repeat periodically in three directions.
A soapfilm bounded by a skew quadrilateral. Illustrates fixed vertices and
edges. This is as simple as it gets.
A spinning liquid drop on a circular rod. Assuming an equatorial symmetry
plane, only the top half is actually computed (first image). The evolved
equilibrium shape for this particular spin (second image) is unstable, with
two modes of instability, each of multiplicity two due to circular symmetry.
The third image shows
the most unstable mode, a bulging to one side, and the last image shows
the other unstable mode, a bar shape.
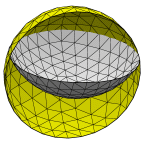A partially filled spherical tank, with a contact angle of 45 degrees
between the liquid surface and the tank wall. The tricky part of this
example is handling the gaps between the straight edges of the liquid
surface facets and the curved wall of the tank.
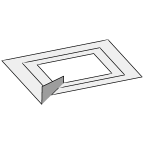
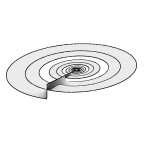A simple closed curve that bounds uncountably many different soap films.
Each lane of the spiral may or may not have a film, and since there are
infinitely many lanes, there are uncountably many subsets of lanes to fill.
This film follows the repeating pattern of two full lanes, one empty lane.
The Evolver model actually only contains one period of the pattern, and the
image was formed by displaying four copies suitably sized.
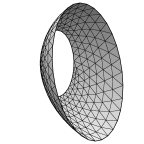A partially filled cylindrical tank with a horizontal axis,
with a contact angle of 30 degrees
between the liquid surface and the tank walls. Gravity is acting downward.
Only the liquid surface is shown. The liquid forms an annulus in one end
of the tank.
The tricky part of this example is handling the gaps between the straight edges of the liquid
surface facets and the curved wall of the tank.
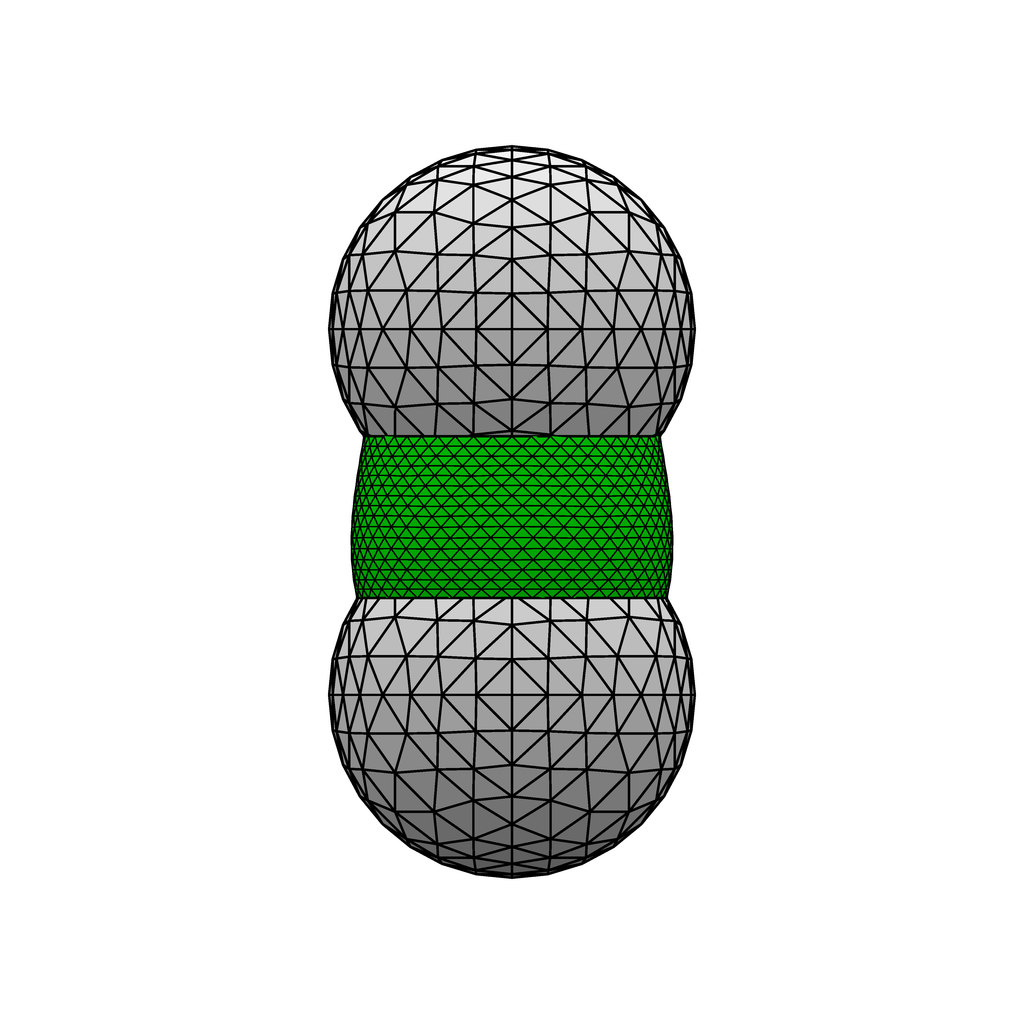Two vertically stacked spheres with a liquid bridge between them. The spheres' heights, radii, and contact
angles are all adjustable in the datafile. Constraint integrands are use in the main datafile,
TwoSpheres.fe
and a document giving the derivation of the integrands is
TwoSpheres.fe.
An auxiliary datafile with explicit contact facets instead of constraint integrands is
TwoSpheres.fe,
as a means of checking that the constraint integrands are correct.
A foam of 14-sided polyhedra, called Kelvin's Tetrakaidecahedra. The Evolver
model actually consists of two polyhedra in a unit cube, with the opposite
faces identified in what is called the 'torus model'. This foam has been
beaten for efficient space-filling.
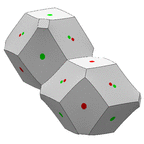A Williams cell foam, draped over balls inside the cells. More
here.
Micro chips flipped up by surface tension forces
of liquid solder.
Surface Evolver home page
Ken Brakke's home page
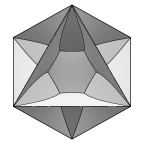Octahedral films page
Triply Periodic Minimal Surfaces page
