Triply Periodic Minimal Surfaces
A minimal surface is a surface that is locally area-minimizing,
that is, a small piece has the smallest possible area for a surface
spanning the boundary of that piece. Soap films are minimal surfaces.
Minimal surfaces necessarily have zero mean curvature, i.e. the sum
of the principal curvatures at each point is zero. Particularly
fascinating are minimal surfaces that have a crystalline structure, in
the sense of repeating themselves in three dimensions, in other words
being triply periodic. Many triply periodic minimal surfaces are known,
some of which are pictured on this page.
These images were made with the
Surface Evolver.
The Evolver datafiles are the *.fe files linked to below. The surfaces
are generally made by defining and evolving the fundamental region of
the surface, which is usually very simple due to the high symmetry, and
then displaying many copies of it, suitably transformed.
The fundamental regions usually are one of Coxeter's
kaleidoscopic cells.
Surfaces with "adj" in the file name were made by evolving the
adjoint surface. These surfaces need the
Evolver file adjoint.cmd.txt along with the
datafile.
NOTE: Many of these files also need the file cube_transforms.inc, which
contains the transformations for showing multiple copies of the fundamental region. (The downloaded file is actually
named cube_transforms.inc.txt, since our university web server will only permit certain extensions on
downloaded files. Remove the ".txt" extension after downloading.)
Many of these surfaces were originally discovered by Alan Schoen in his famous
1970 NASA technical report Infinite Periodic Minimal Surfaces without Self-Intersection (also here).
I have made plastic models of several of these using 3D printing via
Shapeways.com. These models
are available for public purchase from Shapeways; see my
list.
Some of the images below made the
cover of AMS Notices in December, 2000.
Edo Timmermans makes triply periodic minimal surfaces out of magnetic
balls. See his videos of the P-surface,
D-surface,
H-surface, and more.
Genus
The genus numbers reported for these minimal surfaces are for the compact surface resulting from
identifying the opposite faces of a unit cell. The Evolver models of the surfaces are not set
up that way, i.e. they are not in the "torus model". So one cannot calculate the Euler index
of a cubic unit cell with the Evolver expression "vertex_count - edge_count + facet_coumt".
Instead, edges on the border of the surface count as only half an edge in Euler's formula,
since two such edges are identified as one edge in the compact surface. And likewise corner
vertices count 1/4 for a 90 degree corner, 1/6 for a 60 degree corner, 1/8 for a 45 degree
corner, etc. Edges along an interior portion of the border count 1/2. Note that doubling
the size of the unit cell doubles the Euler index, but does not quite double the genus
( recall V - E + F = 2(1-g) ).
Contents:
|
|
|
|
|
|
Quadrilateral
before evolving.
| Quadrilateral
after evolving.
| Unit cubic cell
showing mirror planes.
| Four unit cubes.
| Unit cubic cell
showing embedded
straight C2 axes.
| A unit made
of a catenoid
between squares.
|
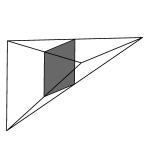
Schwarz' P Surface
The fundamental region, as bounded by mirror planes, is a
quadrilateral in a tetrahedron which is 1/48 of a cube.
The left two images show the fundamental region before and after
evolution. The third image is one cubical unit cell, and the fourth is
four unit cells. The fundamental quadrilateral has a C2 axis (straight line with
180 degree rotation symmetry), and the fifth image shows all the embedded C2 axes.
The surface divides space into two congruent
labyrinths, as do many of the other surfaces on this page.
Evolver file: pcell.fe
Buy from Shapeways.com
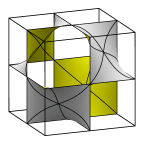
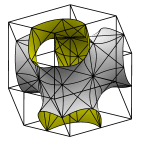
Schwarz' D Surface
The left image shows a cubical unit cell. Note that the translation period
of the labyrinths is twice that of the surface itself; i.e. a unit
translation of the surface switches the sides of the surface.
The middle image shows an alternate unit cell.
The right shows the surface
in a rhombic dodecahedron. The skeletons of the labyrinths have a diamond
lattice pattern, which gives the surface its name.
Small metal sculptures of the D surface are available from
Bathsheba Sculpture.
Evolver file: dcell.fe
Buy from Shapeways.com
Schoen's Gyroid Surface
The gyroid has three-fold rotational
symmetry but no embedded straight lines or mirror symmetries. It is locally
isometric to both the P and D surfaces, being an intermediate in the
Bonnet rotation family of the P and D surfaces. More on my
gyroid page.
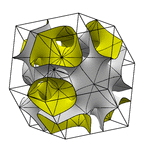
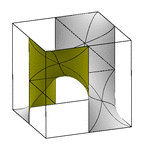
Schoen's Complementary D Surface
This surface has the same space symmetry group and same straight
lines as Schwarz's D surface. If you look carefully at the left, you will see that
the piece shown does not have full 6-fold rotational symmetry; a 1/6
rotation requires a flip. The right image shows a rhombic dodecahedron unit cell. For more on this and related surfaces, go
here.
Evolver file: cd.fe
Buy from Shapeways.com
(rhombic dodecahedron unit cell, fine mesh)
Buy from Shapeways.com
(rhombic dodecahedron unit cell, coarse mesh)
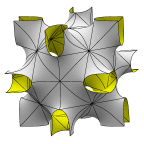
Neovius' Surface
A cubical unit cell, basically a central chamber with necks out to the middle of
each edge of the cube.
Evolver file: neovius.fe
Buy from Shapeways.com
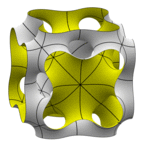
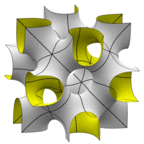
N14 Surface
One version of the cubical unit cell basically a central chamber with necks out to the middle of
tubues running along each edge of the cube. Another cubical unit cell, offset from the first
by half an edge in each direction, looks like a Neovius surface with extra tunnels. Genus 14.
For lack of a better name, I am calling this "N14" for "Neovius genus 14". Proposed by Alan
Schoen from sketches he dug up from 1969.
Evolver file: N14.fe
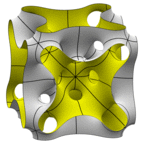
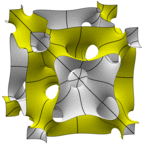
N26 Surface
This is the N14 surface with some extra holes I punched in it to make it genus 26. Again, two
different unit cells are shown.
Evolver file: N26.fe
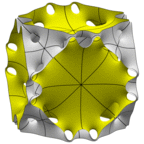
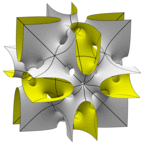
N38 Surface
This is the N14 surface with some extra holes I punched in it a different way to make it genus 38. Again, two
different unit cells are shown.
Evolver file: N38.fe
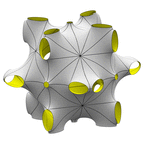A family of surfaces generalizing the Neovius surface.
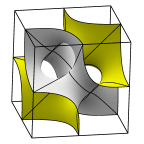Surfaces having a quadrirectangular tetrahedron as kaleidoscopic cell.
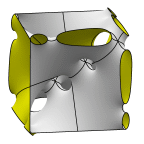This is a two-parameter family, members of which are shown in tables of
kaleidoscopic cells,
cubelets, and
rhombic dodecahedra,
labeled by their genus.
The family may be parameterized by (p,q), where p is the number of
holes along the cube edge, and q along the cube diagonal.
Pictured at left is (3,3).
Putative members of the family
may not actually exist; attempts
to get all the edges of the fundamental region to match up properly
(called "period killing" by the cognoscenti) may leave a gap.
Starfish 4-2
fails to period kill by only 0.005 (so far).
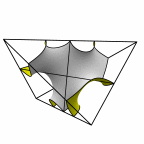Several families of surfaces whose kaleidoscopic cell is the
tetragonal disphenoid. There are two C2 axes, of unequal length.
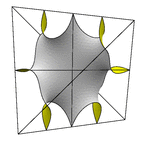
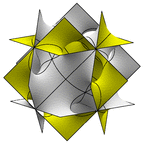
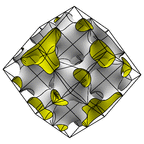A disphenoid surface, using two C2 axes of equal length. This surface has the same skeleton of
embedded straight lines as the P surface and Neovius' surface (middle). At right is a rhombic cell.
Evolver file: P3a.fe
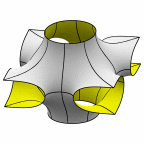Some combination surfaces.
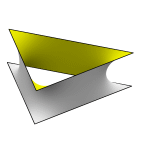
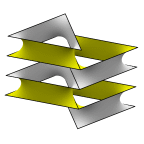
Schwarz' H Surface
The left image shows a equilateral triangular prism cell, which is
actually half of a lattice unit cell.
The right shows four cells connected.
Evolver file: hcell.fe
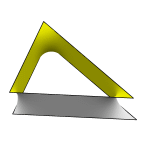
Schoen's RII Surface
The image shows an isosceles right triangular prism cell, which again
is half of a lattice unit cell.
Evolver file: RII.fe
Schoen's RIII Surface
The image shows a 30-60-90 triangular prism cell, once more half
of a lattice unit cell.
Evolver file: RIII.fe
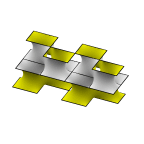
Schoen's I-6 Surface
Surface between plane square grids.
Evolver file: I-6.fe
Schoen's I-8 Surface
Surface between plane square grids with diagonals.
Evolver file: I-8.fe
Schoen's I-9 Surface
Another surface between plane square grids with diagonals.
Evolver file: I-9.fe
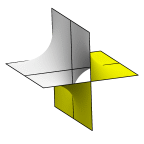
Schwarz' CLP Surface
This surface can be viewed as two orthogonal sets of parallel planes
with alternating tunnels through the intersections to remove the
lines of intersection.
Evolver file: CLP.fe
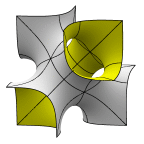
Schoen's F-RD Surface
Unit cell with tetrahedral symmetry. It may be viewed as a central
chamber with tubes to alternating corners of the cube.
This is actually only an eighth of a lattice cell; to get a lattice cell,
reflect in the cube faces.
Evolver file: FRDadj.fe
Buy from Shapeways.com
(unit cell)
Buy from Shapeways.com
(1/8 unit cell)
![Hybrid-1[P,F-RD] surface](hybrid-1/hybrid-1cube.2.gif)
Schoen's Hybrid-1[P,F-RD] Surface
Unit cell with tetrahedral symmetry. It may be viewed as a central
chamber with tubes to alternating corners of the cube and to the faces of the cube.
This is actually only an eighth of a lattice cell; to get a lattice cell,
reflect in the cube faces.
Evolver file: hybrid-1adj.fe
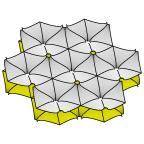
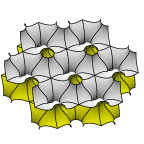
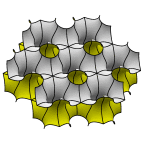
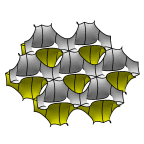
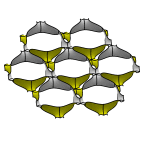
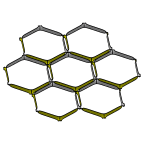
Schoen's GW Surface
One labyrinth of this surface has the graphite hexagonal sheet structure,
and the other labyrinth has the wurtzite structure, hence the name GW.
As a parameter is varied from small (left) to large (right), the surface
goes from horizontal parallel sheets with catenoid connections to
pairs of vertical sheets in a hexagonal layout with cross-tunnels at
the junctions.
Evolver file: GW5adj.fe
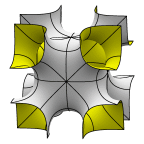
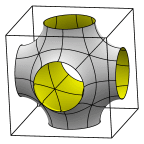
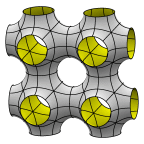
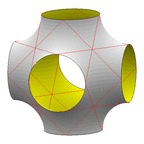
Schoen's I-WP Surface
The unit cell may be viewed as a central
chamber with tubes to the corners of the cube.
Evolver file: IWP.fe
Buy from Shapeways.com
(1/8 unit cell)
Buy from Shapeways.com(full unit cell)
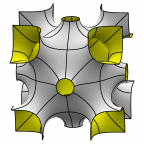
Schoen's O,C-TO Surface
The unit cell may be viewed as a central
chamber with tubes to the corners and faces of the cube, thus being a
hybrid of the P surface and the I-WP surface.
Evolver file: octoadj.fe
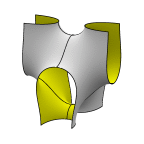
Schoen's F-RD(r) Surface (formerly unnamed Surface 12)
The unit cell may be viewed as a chamber in a box with tubes running to the
centers of four edges. The unit cell has 8-fold symmetry (there being
horizontal C2 axes as well as the mirror lines shown). The box is square
based, and the height is variable. The cell shown is actually only half
of a lattice cell; reflect in the top or bottom cube face to get a full
lattice cell. This image was actually constructed
by evolving the adjoint surface
(which is in the datafile), adjusting a
parameter to kill one period, and then doing an adjoint transformation.
Evolver file: s12adj.fe
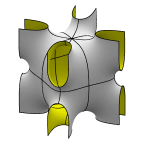
Schoen's I-WP(r) Surface (formerly unnamed Surface 14)
The unit cell may be viewed as a chamber in a box with tubes running to the
centers of eight edges. The unit cell has 16-fold symmetry.
The box is square
based, and the height is variable. This image was actually constructed
by evolving the adjoint surface
(which is in the datafile), adjusting a
parameter to kill one period, and then doing an adjoint transformation.
Evolver file: s14adj.fe
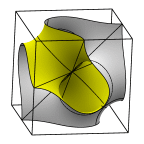
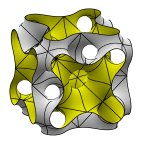
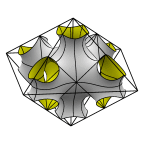
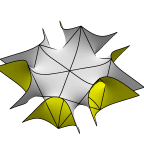
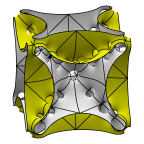
Schoen's Manta Surface of Genus 19
The fundamental region is a tetrahedron which is 1/96 of a cube.
The left image shows two fundamental regions, whose appearance is the
source of the name "manta". The second image shows 12 fundamental
regions in a cube.
The third image is the full cubical unit cell.
The fourth image shows the surface as a chamber with tubes in a
slightly flattened octahedron.
Evolver file: mantaadj.fe
Buy from Shapeways.com
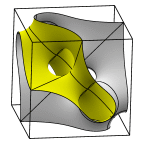
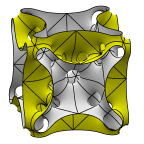
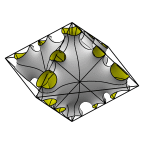
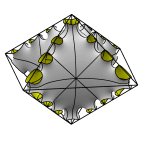
Schoen's Manta Surface of Genus 35
The second member in the Manta series.
Evolver file: manta35adj.fe
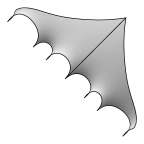
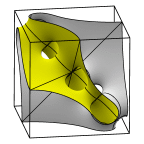
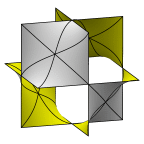
Schoen's Manta Surface of Genus 51
The third member in the Manta series.
Evolver file: manta51adj.fe
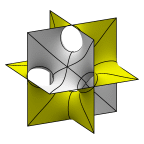
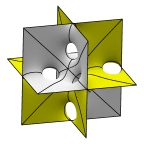
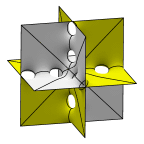
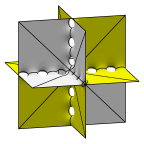
A sequence of surfaces converging to three sets of orthogonal planes.
One intuitive way to construct a lot of minimal surfaces is to
take a set of minimal surfaces and resolve their intersections
to smooth surfaces by drilling tunnels crosswise. This sequence,
starting with the D surface, shows lattice cells of the surface.
Note the labyrinth periods are twice the surface periods.
The surfaces are of genus 3, 9, 15, 21, 27, and 33.
Evolver files:
triplane0adj.fe,
triplane1adj.fe,
triplane2adj.fe,
triplane3adj.fe,
triplane4adj.fe,
triplane5adj.fe
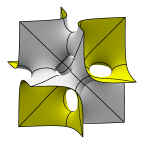
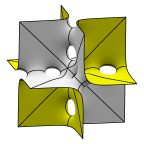
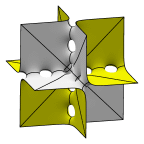
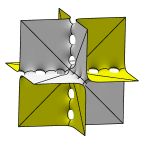
A sequence of surfaces converging to three sets of orthogonal planes,
beginning with the F-RD surface,
which intercalates the sequence above. Each cube pictured here
is actually 1/8 of the lattice cell.
The surfaces are of genus 6, 12, 18, 24, and 30.
Evolver files:
hexplane1adj.fe,
hexplane2adj.fe,
hexplane3adj.fe,
hexplane4adj.fe,
hexplane5adj.fe
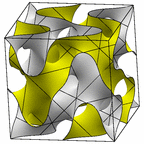
Fischer-Koch S Surface
Left: Piece of the Fischer-Koch S surface. The piece is bounded by straight lines,
which are axes of 180 degree rotation symmetry in the directions of the diagonals of
the faces of a cube. Right: a cubic unit cell. Note that this surface has no mirror
symmetry, so the sides of the cube are not mirror planes. There is a C3 axis down one
diagonal of the cube
Evolver file: Scell.fe
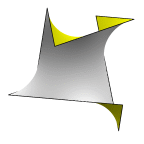
Fischer-Koch C(S) Surface
Piece of the Fischer-Koch C(S) surface which they later realized was the same as the P surface. The piece is bounded by straight lines,
which are axes of 180 degree rotation symmetry.
Evolver file: CScell.fe
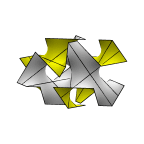
Fischer-Koch Y Surface
At left is a piece of the Fischer-Koch Y surface, which they later realized
is the same as the D surface. The piece is bounded by straight lines,
which are axes of 180 degree rotation symmetry. At right is a bunch of
pieces together, producing two labyrinths of tunnels.
Evolver file: ycell.fe
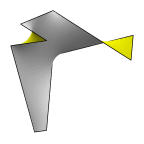
Fischer-Koch C(Y) Surface
Piece of the Fischer-Koch C(Y) surface. The piece is bounded by straight lines,
which are axes of 180 degree rotation symmetry.
Evolver file: CYcell.fe
Back to
Surface Evolver examples.
Back to
Ken Brakke's home page.
![Hybrid-1[P,F-RD] surface](hybrid-1/hybrid-1cube.8.gif)
