Triply Periodic Minimal Surfaces - Batwing Family

This page presents several families of triply periodic minimal surfaces that have the quadrirectangular tetrahedron (1/48 of a cube) as their kaleidoscopic cell, with a C2 symmetry axis.

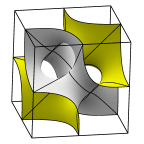
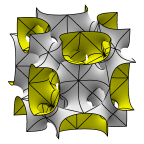
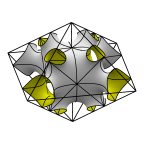
batwing pair batwing cube batwing cell batwing octahedron

Schoen's Batwing Surface

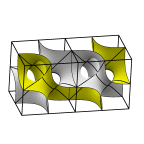
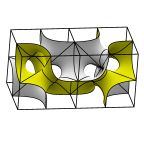
The left image shows two fundamental regions, whose appearance is the source of the name "batwing". The two fit in a tetrahedron, which is 1/48 of a full lattice cell cube. The second image shows 12 fundamental regions in a cube. This appears to the eye to be a lattice fundamental cell, but it is not. Opposite edges almost match under translation, but there are actually gaps of about .02. The third image is the full cubical unit cell. The fourth image shows the surface as a chamber with tubes in a slightly flattened octahedron. The genus of this surface is 25.
Evolver file: batwingadj.fe
Buy from Shapeways.com (unit cell)
Buy from Shapeways.com (1/8 unit cell)
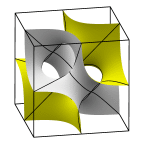
pseudo-batwing cube pseudo-batwing pair batwing two piece

Brakke's Pseudo-Batwing Surface

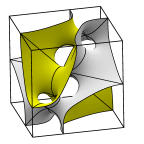
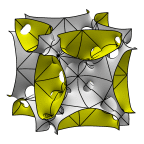
This is the surface suggested by the near-symmetry of the small batwing cube. The left image shows a full lattice fundamental cell. The difference from the corresponding batwing piece is the cube face mirror symmetry planes are replaced by C2 axes on the cube face diagonals. The middle image shows two pseudo-batwing cells, and the right image shows the corresponding two batwing cubes, for easy comparison.
Evolver file: pbatadj.fe
Buy from Shapeways.com (1/8 unit cell)
batwing41 pair batwing41 cube batwing41 cell batwing41 octahedron

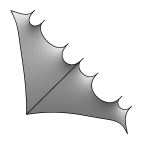
Schoen's Batwing-41 Surface

This is a higher genus version of the Batwing surface, with genus 41. The left image shows two fundamental regions, whose appearance is the source of the name "batwing". The middle image shows 12 fundamental regions in a cube. The third image is the full cubical unit cell. The fourth image shows the surface as a chamber with tubes in a slightly flattened octahedron.
Evolver file: batwing41adj.fe
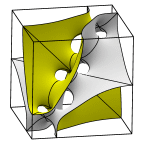
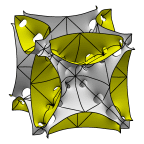
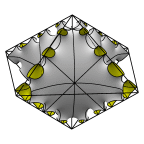
batwing57 pair batwing57 cube batwing57 cell batwing57 octahedron

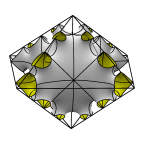
Schoen's Batwing-57 Surface

This is a higher genus version of the Batwing surface, with genus 57. The left image shows two fundamental regions, whose appearance is the source of the name "batwing". The middle image shows 12 fundamental regions in a cube. The third image is the full cubical unit cell. The fourth image shows the surface as a chamber with tubes in a slightly flattened octahedron.
Evolver file: batwing57adj.fe
Back to Triply Periodic Minimal Surfaces.
Back to Ken Brakke's home page.