Kaleidoscopic Cells
Many triply periodic minimal surfaces
can best be understood and constructed in terms of fundamental regions
bounded by mirror symmetry planes. According to H. S. M. Coxeter
(Regular Polytopes, p. 84) there are exactly seven types of such
regions of finite size. These are shown here, with commentary
relevant to triply periodic minimal surfaces.
Many triply periodic minimal surfaces have embedded straight lines,
which of necessity must be C2 symmetry axes (180 degree rotational
symmetry). Possible C2 axes are shown in color below.
There are two classes of kaleidoscopic cells: the prisms and the
tetrahedra. A prism in the general sense
is a plane polygon extended at right angles in the third dimension.
A tetrahedron is a polyhedron with four flat faces.
Prisms
|
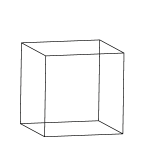
Rectangular Parallelepiped
A rectangular box, shown in its maximally symmetric form of a cube. |

|
|
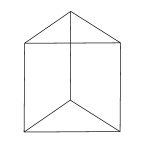
Equilateral Prism
A prism based on an equilateral triangle. |

|
|
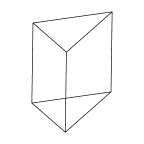
Isosceles Prism
A prism based on a 45-45-90 degree triangle. |

|
|
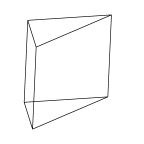
30-60-90 Prism
A prism based on a 30-60-90 degree triangle. |

|
Tetrahedra
|
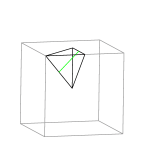
Quadrirectangular Tetrahedron
This tetrahedron is shown as 1/48 of a cube; it is the fundamental
region for the full symmetry group of the cube. There is one possible
C2 axis, shown in green. The name quadrirectangular refers
to the fact that each of the four faces has a right angle. |

|
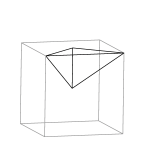
|
Trirectangular Tetrahedron
This tetrahedron is shown as 1/24 of a cube. There are no possible
C2 axes. |

|
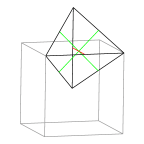
|
Tetragonal Disphenoid
This tetrahedron can be viewed as two trirectangular tetrahedra
stacked up. There are three possible C2 axes, shown in green and red.
| 
|
Back to
periodic minimal surfaces.
Back to
Ken Brakke's home page.










