Adjoint Minimal Surfaces
A minimal surface can undergo an amazing geometric transformation
called a Bonnet rotation in which every surface element maintains
its normal vector but rotates a given angle in its tangent plane.
If and only if the surface is a minimal surface, then the surface
elements all fit together again. The Bonnet rotation is an isometry
of the surface, that is, all distances within the surface are
preserved; there is no stretching or wrinkling. As the Bonnet
rotation angle increases, a continuous family of minimal surfaces
is generated. Minimal surfaces that are ninety degree Bonnet
rotations of each other are called adjoint surfaces.
For example, the catenoid and helicoid are adjoints.
 |
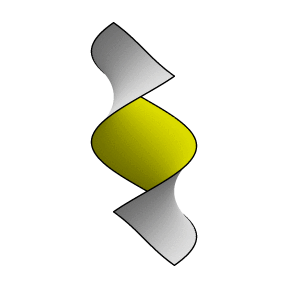 |
 |
| Catenoid, 0o rotation. |
45o rotation. |
Helicoid, 90o rotation. |
A multiply connected surface must be instead treated as its universal
covering surface, as the catenoid-helicoid shows. Hence the adjoint
of a triply periodic minimal surface will not usually be triply
periodic (at least not a non-self-intersecting TPMS). Some pairs
are adjoints, though, such as the P and D surfaces.
An important property of the adjoint transformation is that
mirror planes transform to embedded two-fold rotation axes, and
vice versa. For example, the equator of the catenoid turns into
the midline of the helicoid.
A fact useful for generating TPMS shown in these pages is that the
adjoint of an unstable fundamental region may be stable. All the
free contact lines on the faces of the kaleidoscopic cells transform
to fixed straight line boundaries, which are much more stable.
However, the lengths of those boundaries are unknown a priori; they
must be adjusted to make the surface match up going around a hole.
This is the notorious period killing problem of proving a conjectured
TPMS exists.
A nifty algorithm for the Bonnet rotation of triangulated minimal surfaces
(such as the Surface Evolver produces) was discovered by Pinkall and
Polthier. If each triangle is rotated by the Bonnet angle in its own
plane, the triangles can be translated to be reassembled so the midpoints
of the edges match up again. The edges are not parallel, so the
triangle vertices do not quite match up. Thus the algorithm used
in adjoint.cmd puts each vertex at the average position of all its
images. To see a movie of such a Bonnet rotation on a patch with just
a few facets (to better see how the facets wind up "nonconforming"),
click here (1.4 MB).
To see a movie of a many-thousand facet fundamental region of a
Starfish surface, click
here (1.6 MB).
My algorithm for computing a TMPS by its adjoint is as follows:
- Set up the adjoint in a datafile with parameters for the
adjustable edge lengths. Included is a command that calculates
the approximate periods directly in the adjoint.
- Repeatedly evolve and adjust the edge lengths to nearly kill all the
periods.
- Transform to the adjoint, replacing with each fixed edge with
a constraint plane. Note that unkilled periods mean several parallel
planes where there is supposed to be one plane face of the kaleidoscopic
cell.
- Use the Evolver's hessian command to get the exact minimal surface.
The minimal surface is unstable (usually the index is the same as
the number of periods to kill), so ordinary gradient descent evolution
doesn't work. But hessian seeks the equilibrium surface, so it works
as long as the starting surface is near the equilibrium.
- Gradually move the constraint planes into alignment, using hessian
to keep the surface minimal.
Return to Triply Periodic Minimal Surfaces





