Triply Periodic Minimal Surfaces - Disphenoid Surfaces
This page presents several families of
triply periodic minimal surfaces that
have the
tetragonal disphenoid
as their kaleidoscopic cell, with short and long C2 symmetry axes.
NOTE: What is referred to below as a "cubic unit cell" is a unit cell for the
unoriented surface; the oriented unit cell is twice as big, and is shown as a rhombic
dodecahedron. The genus numbers are for the oriented unit cell.
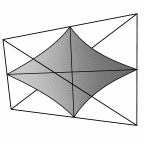
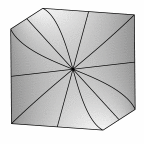
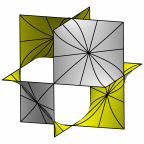
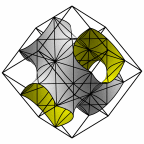
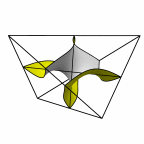
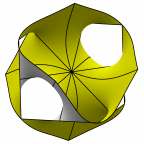
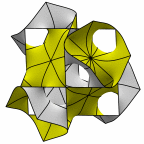
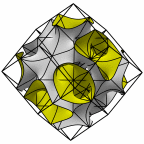
Schwartz' D surface - genus 3
At left is four fundamental regions in a disphenoid, with two C2 axes.
At mid left, twelve fundamental regions form a cubelet. At mid right is a cubic
unit cell formed from four cubelets. At right is a rhombic dodecahedron made
of 24 disphenoids.
Evolver file: dcell.fe
Family A
This family progressively introduces a new edge along the long side of
the disphenoid.
Schoen's complementary D surface - genus 19
At left is four fundamental regions in a disphenoid, with two C2 axes.
At mid left, twelve fundamental regions form a cubelet. At mid right is a cubic
unit cell formed from four cubelets. At right is a rhombic dodecahedron made
of 24 disphenoids.
Evolver file: disphenoid19.fe
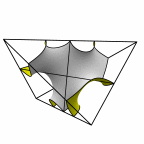
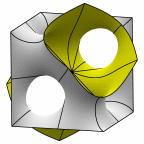
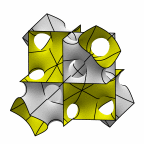
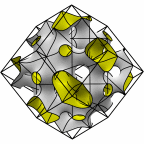
New disphenoid surface - genus 31
At left is four fundamental regions in a disphenoid, with two C2 axes.
At mid left, twelve fundamental regions form a cubelet. At mid right is a cubic
unit cell formed from four cubelets. At right is a rhombic dodecahedron made
of 24 disphenoids.
Evolver file: disphenoid31adj.fe
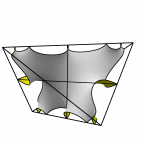
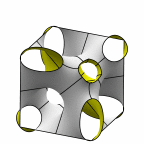
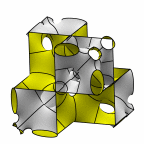
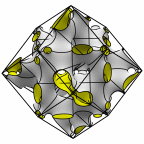
New disphenoid surface - genus 43
The next member in the family of the previous surface.
At left is four fundamental regions in a disphenoid, with two C2 axes.
At mid left, twelve fundamental regions form a cubelet. At mid right is a cubic
unit cell formed from four cubelets. At right is a rhombic dodecahedron made
of 24 disphenoids.
Evolver file: disphenoid43adj.fe
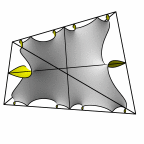
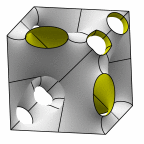
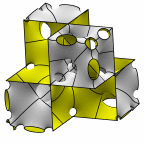
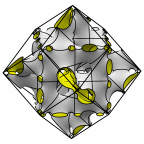
New disphenoid surface - genus 55
The next member in the family of the previous surface.
At left is four fundamental regions in a disphenoid, with two C2 axes.
At mid left, twelve fundamental regions form a cubelet. At mid right is a cubic
unit cell formed from four cubelets. At right is a rhombic dodecahedron made
of 24 disphenoids.
Evolver file: disphenoid55adj.fe
Family B
This family progressively introduces a new edge along the short side of
the disphenoid.




Schoen's complementary D surface - genus 19
At left is four fundamental regions in a disphenoid, with two C2 axes.
At mid left, twelve fundamental regions form a cubelet. At mid right is a cubic
unit cell formed from four cubelets. At right is a rhombic dodecahedron made
of 24 disphenoids.
Evolver file: disphenoid19.fe
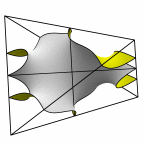
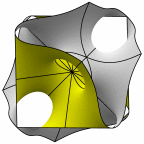
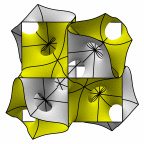

New disphenoid surface - genus 35
At left is four fundamental regions in a disphenoid, with two C2 axes.
At mid left, twelve fundamental regions form a cubelet. At mid right is a cubic
unit cell formed from four cubelets. At right is a rhombic dodecahedron made
of 24 disphenoids.
Evolver file: disphenoid35adj.fe
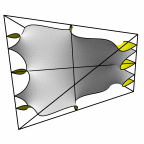
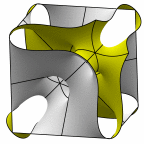
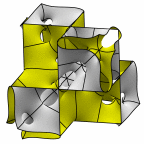
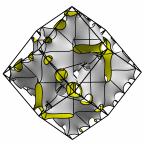
New disphenoid surface - genus 51
At left is four fundamental regions in a disphenoid, with two C2 axes.
At mid left, twelve fundamental regions form a cubelet. At mid right is a cubic
unit cell formed from four cubelets. At right is a rhombic dodecahedron made
of 24 disphenoids.
Evolver file: disphenoid51adj.fe
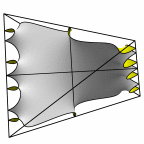
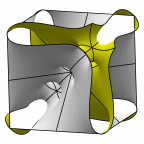
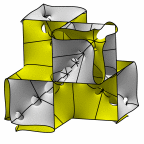
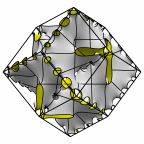
New disphenoid surface - genus 67
At left is four fundamental regions in a disphenoid, with two C2 axes.
At mid left, twelve fundamental regions form a cubelet. At mid right is a cubic
unit cell formed from four cubelets. At right is a rhombic dodecahedron made
of 24 disphenoids.
Evolver file: disphenoid67adj.fe
Back to
Triply Periodic Minimal Surfaces.
Back to
Ken Brakke's home page.



































