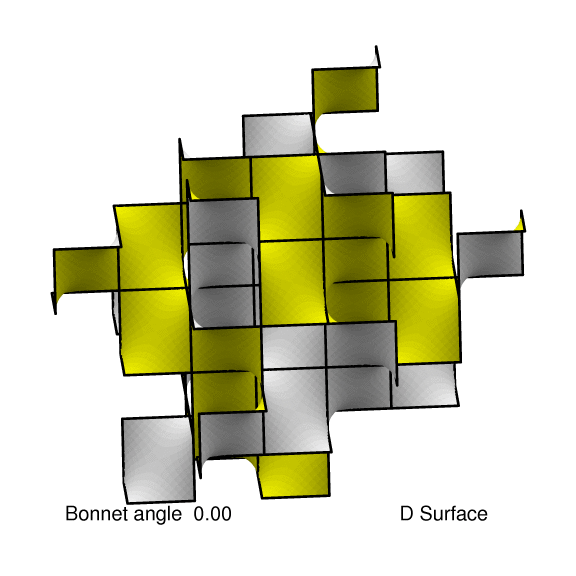
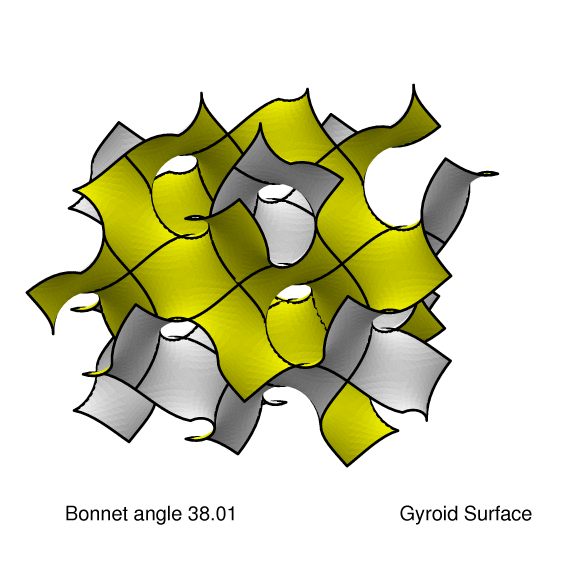
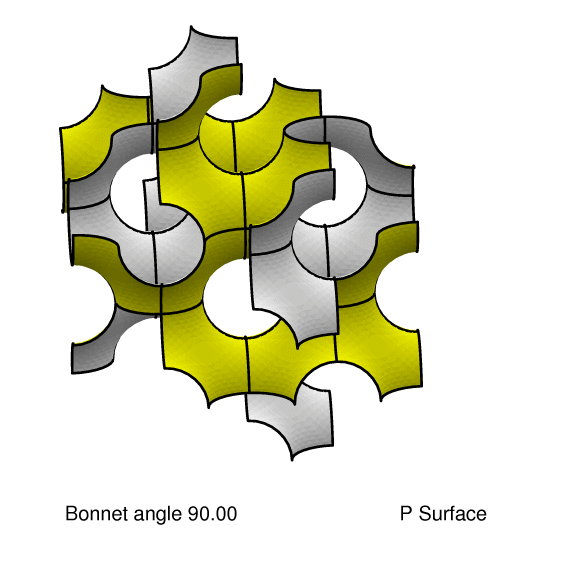
in the sense of being a Bonnet rotation of the D-surface by
38.0147739891081 degrees, while the P-surface is a Bonnet
rotation by 90 degrees (play movie). Thus the gyroid is locally isometric to both
the D-surface and the P-surface.
Alan Schoen recently wrote a
description
of his discovery of the gyroid.
|
The gyroid is intermediate between the D-surface and the P-surface in the sense of being a Bonnet rotation of the D-surface by 38.0147739891081 degrees, while the P-surface is a Bonnet rotation by 90 degrees (play movie). Thus the gyroid is locally isometric to both the D-surface and the P-surface. |
|
|
| Small metal sculptures of the gyroid are available from Bathsheba Sculpture |
|
Click on the images for larger versions.
|
A cubic unit cell of the gyroid. Note that the cube faces are not symmetry planes. Genus 5. |
|
A piece of gyroid that is two unit cells in each direction. There is a C3 symmetry axis along the cube diagonal from the upper right corner. |
|
Looking along the C3 axis. |
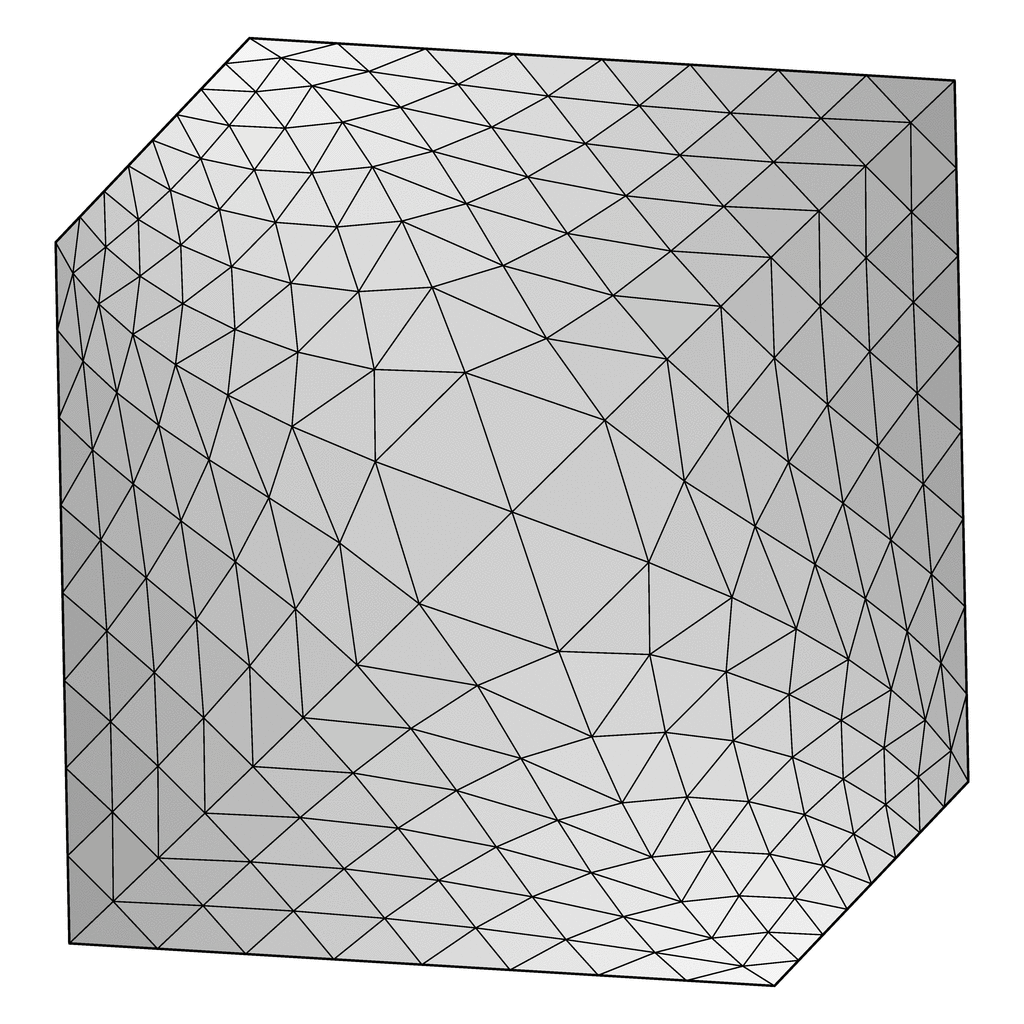
| gyroid-cube.fe A cubic unit cell with a coarsely meshed gyroid. Torus model. With squared mean curvature for energy, so it is stable in evolution. |
| gyroid-hex.fe A hexagonal region of the D surface, with scripts for displaying multiple copies and doing Bonnet rotation. Also contains the scripts for making the movie. You will also need to download gyroid-bdry.txt, since it contains a lot of data included by the datafile. |
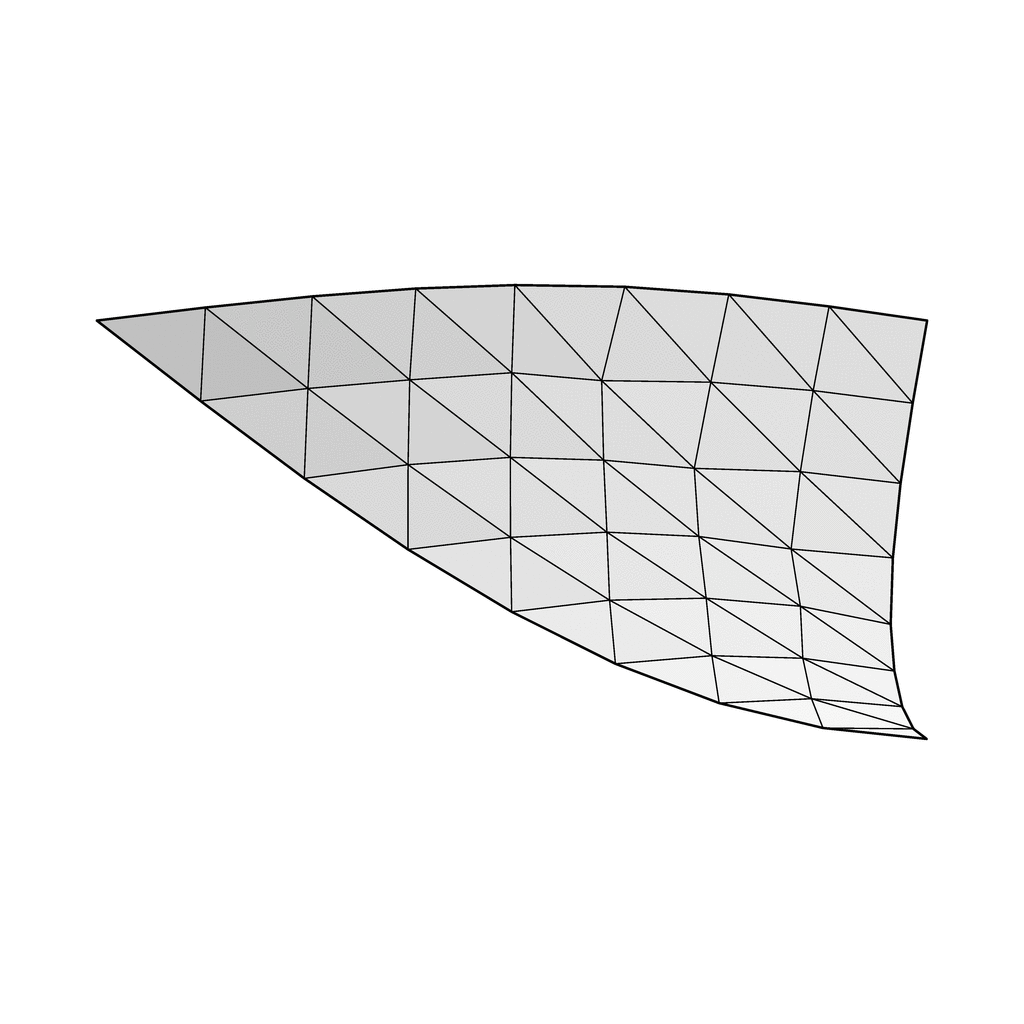
| gyroid-tri.fe A triangular fundamental region of the surface. Comes with three view transform generators, one for each edge, so you can play around making your own patches of surface with the transform_expr command. |
|
| Some hand-picked sets of transforms of the fundamental region triangle. |
| 15views.fe | 42views.fe |