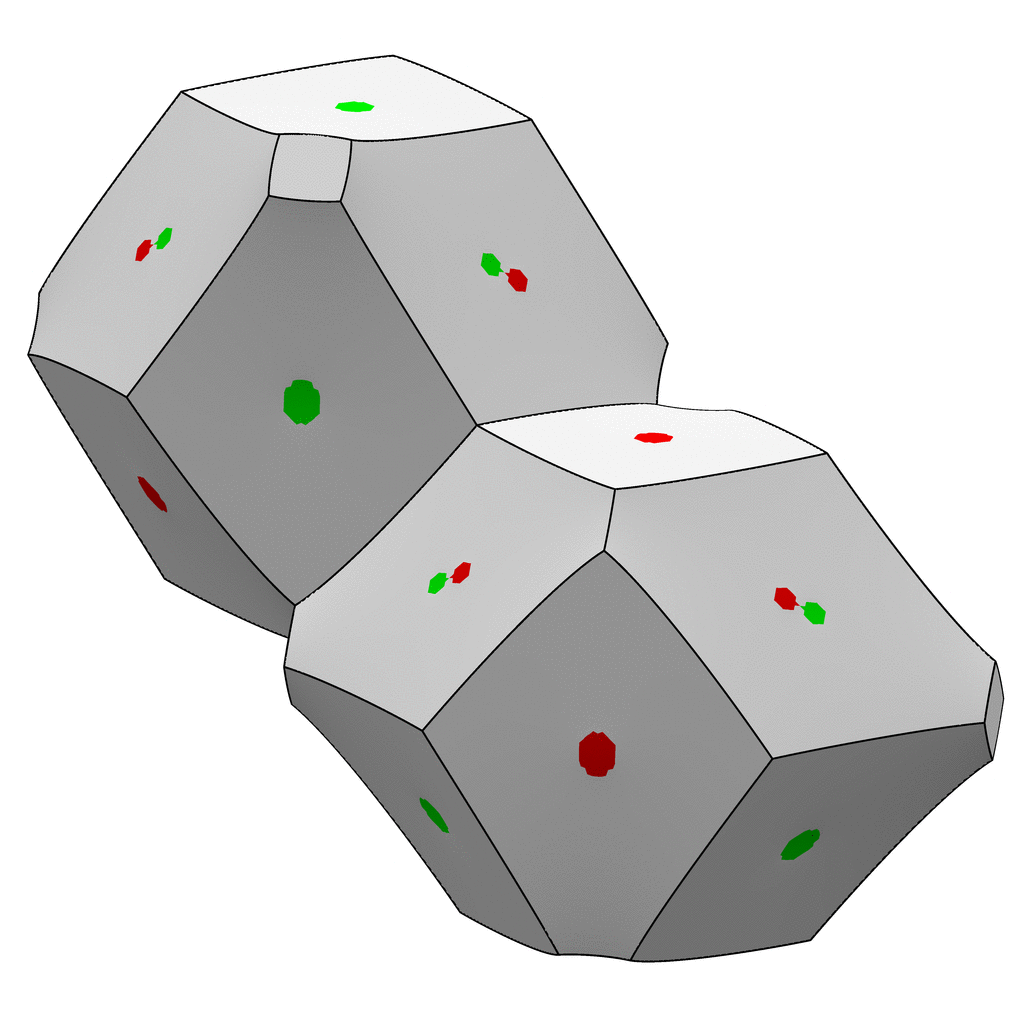
The "Williams cell" is a shape of foam cell that is generated by starting with a rhombic dodecahedron foam (Voronoi regions of a face-centered cubic lattice) and "popping" the vertices to insert small squarish faces in certain orientations, so Plateau's Laws are satisfied. This particular example explores the question of what happens when solid balls are placed in the centers of the Williams cells; do the soap films manage to avoid the balls (except for points where the balls touch), as is true for the Kelvin foam, or do the films drape over the balls? The result shown here demonstrates that the films do indeed drape over the balls. The red spots are where the film drapes over an interior ball, and the green spots are where it drapes over an exterior ball.
Károly Bezdek has raised the question: What is the minimum-area foam such that each cell contains a unit ball? He proves a lower bound on average cell area of 24/sqrt(3) = 13.8564... for convex cells. For a Kelvin foam with the size scaled to accommodate unit balls, a cell area is 17.82797... . For the draped Williams cell, the cell area is 16.95745... , as compared to 12*sqrt(2) = 16.97056... for the original rhombic dodecahedron foam. So the Williams cell is more spherical then Kelvin in this sense, even though Kelvin beats it on a per-volume basis. It is conjectured that the draped Williams cell is optimal for Bezdek's problem.
Datafile: williams-2-balls.fe. Comes with a script "run" to evolve what is shown here, plus a script "make_pic" to create a PostScript file for this image.