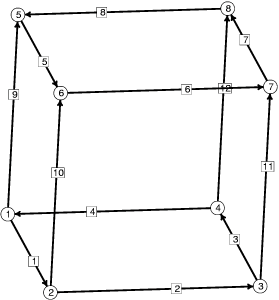
 The initial cube skeleton, with
vertices and edges numbered.
The initial cube skeleton, with
vertices and edges numbered.
 The initial cube skeleton, with
vertices and edges numbered.
The initial cube skeleton, with
vertices and edges numbered.
This is the datafile that specifies the initial unit cube:
// cube.fe // Evolver data for cube of prescribed volume. vertices /* given by coordinates */ 1 0.0 0.0 0.0 2 1.0 0.0 0.0 3 1.0 1.0 0.0 4 0.0 1.0 0.0 5 0.0 0.0 1.0 6 1.0 0.0 1.0 7 1.0 1.0 1.0 8 0.0 1.0 1.0 edges /* given by endpoints */ 1 1 2 2 2 3 3 3 4 4 4 1 5 5 6 6 6 7 7 7 8 8 8 5 9 1 5 10 2 6 11 3 7 12 4 8 faces /* given by oriented edge loop */ 1 1 10 -5 -9 2 2 11 -6 -10 3 3 12 -7 -11 4 4 9 -8 -12 5 5 6 7 8 6 -4 -3 -2 -1 bodies /* one body, defined by its oriented faces */ 1 1 2 3 4 5 6 volume 1 // end of cube.feThe datafile is organized in lines, with one geometric element defined per line. Vertices must be defined first, then edges, then faces, then bodies. Each element is numbered for later reference in the datafile.
Comments are delimited by /* to begin
and */ to close
as in C, or from // until the end of the line as in C++.
Case is not significant, and all input is made
lower-case immediately. Hence error messages
about your datafiles will refer to items in lower
case, even when you typed them in upper case.
The datafile syntax is based on keywords. The
keywords VERTICES, EDGES, FACES, and
BODIES signal the start of the respective sections.
Note that the faces are not necessarily triangles
(which is why they are called FACES
and not FACETS).
Any non-triangular face will be automatically
triangulated by putting a vertex at its center and
putting in edges to each of the original vertices.
Faces don't have to be planar. Note that a minus
sign on an edge means that the edge is traversed
in the opposite direction from that defined for it in the
EDGES section. A face's oriented normal is defined
by the usual right hand rule. The cube faces all have
outward normals, so they all are positive in the body list.
In defining a body, the boundary
faces must have outward normals. If a face as
defined has an inward normal, it must be listed
with a minus sign.
That the body is constrained to have a volume of 1
is indicated by the keyword VOLUME after the body
definition, with the value of the volume following.
Any attributes or properties an element
has are given on the same line after its definition.
Start Evolver and load the datafile with the command line
evolver cube.fe
You should get a prompt
Enter command:
Give the command s to
show the surface. You should see a square divided into
four triangles by diagonals. This is the front side
of the cube; you are looking in along the positive x-axis,
with the z axis vertical and the positive y axis to the right.
On most systems, you can manipulate the displayed surface with the
mouse: dragging the mouse over the surface with the left button
down rotates the surface; you can change to "zoom" mode by hitting
the z key, to "translate" by hitting t, to "spin" by hitting c, and
back to "rotate" by hitting r. Hit the 'h' key with the mouse focus
in the graphics window to get a summary of the possibilities.
You can also give graphics commands at the graphics command prompt;
this is good for precise control. The graphics command prompt is
Graphics command:
It takes strings of letters, each letter making a
viewing transformation on the surface:
The most used ones are
r rotate right by 6 degrees l rotate left by 6 degrees u rotate up by 6 degrees d rotate down by 6 degrees R reset to original position q quit back to main command promptTry typing
rrdd to get an oblique view of the cube. Any
transformations you make will remain in effect the next
time you show the surface. Now do q to get back to
the main prompt.
If you are using geomview for graphics, do command P
option 8 to get
a display, or just "P 8" for short.
Geomview takes a couple of seconds to initialize.
You can manipulate the geomview display as usual
independently of the Evolver. Evolver will automatically update
the image whenever the surface changes.
Now do some iterations. Give the command "g 5" to do
5 iterations. You should get this:
5. area: 5.11442065156005 energy: 5.11442065156005 scale: 0.186828 4. area: 5.11237323810972 energy: 5.11237323810972 scale: 0.21885 3. area: 5.11249312304592 energy: 5.11249312304592 scale: 0.204012 2. area: 5.11249312772740 energy: 5.11249312772740 scale: 0.204386 1. area: 5.11249312772740 energy: 5.11249312772740 scale: 0.0416708 Enter command:Note that after each iteration a line is printed with the iterations countdown, area, energy, and current scale factor. By default, the Evolver seeks the optimal scale factor to minimize energy. At first, there are large motions, and the volume constraint may not be exactly satisfied. There may be an energy increase due to the volume constraint taking hold. At the end, the scale is 0 because the surface has converged as well as it can at this coarse a triangulation. (Different systems may not give a zero scale here due to numerics.) Volume constraints are not exactly enforced, but each iteration tries to bring the volume closer to the target. Here that results in increases in area. You can find the current volumes with the v command:
Body target volume actual volume pressure 1 1.000000000000000 0.999999779366360 3.408026016427987The pressure in the last column is actually the Lagrange multiplier for the volume constraint. Now let's refine the triangulation with the r command. This subdivides each facet into four smaller similar facets. The printout here gives the counts of the geometric elements and the memory they take:
Vertices: 50 Edges: 144 Facets: 96 Facetedges: 288 Memory: 27554Iterate another 10 times:
10. area: 4.908899804670224 energy: 4.908899804670224 scale: 0.268161 9. area: 4.909526310166165 energy: 4.909526310166165 scale: 0.204016 8. area: 4.909119925577212 energy: 4.909119925577212 scale: 0.286541 7. area: 4.908360229118204 energy: 4.908360229118204 scale: 0.304668 6. area: 4.907421919968726 energy: 4.907421919968726 scale: 0.373881 5. area: 4.906763705259419 energy: 4.906763705259419 scale: 0.261395 4. area: 4.906032256943935 energy: 4.906032256943935 scale: 0.46086 3. area: 4.905484754688263 energy: 4.905484754688263 scale: 0.238871 2. area: 4.904915540917190 energy: 4.904915540917190 scale: 0.545873 1. area: 4.904475138593070 energy: 4.904475138593070 scale: 0.227156You can continue iterating and refining as long as you have time and memory.
Eventually, you will want to quit. So give the q command. You get
Enter new datafile name (none to continue, q to quit):
You can start a new surface by entering a datafile name
(it can be the same one you just did, to start over), or
continue with the present surface by hitting ENTER with
no name (in case you pressed q by accident, or suddenly
you remember something you didn't do), or you can really
quit with another q.