The drop starts as a cube with one face (face 6 of the cube example) on the tabletop (the z = 0 plane). The most straightforward way to specify a contact angle is to declare face 6 to be constrained to stay on the tabletop and give it a surface tension different than the default of 1. But this leads to problems described below. The way the contact angle is handled instead is to omit face 6 and give the edges around face 6 an energy integrand that results in the same energy we would get if we did include face 6. If we let the interface energy density for face 6 be T, then we want a vectorfield w such that
/ /
| T k . dS = | w . dl
/ face 6 / bdry of face 6
So by Green's Theorem,
all we need is curl w = Tk, and I will use
w = -Tyi. Here i j k are the standard
unit basis vectors.
In practice, I don't think about
Green's Theorem as such; I just write down a line integral
that sums up strips of surface.
I have chosen to parameterize the contact angle as the angle
in degrees between the table and the surface on the interior
of the drop. This angle can be adjusted by assigning a new
value to the variable "angle" at runtime.
I could have made WALLT the parameter
directly, but then I wouldn't have had an excuse to show
a macro.
 |
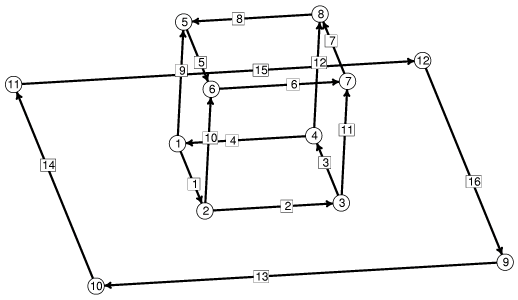
The initial mound skeleton, with vertices and edges numbered. |
mound.fe:
// mound.fe // Evolver data for drop of prescribed volume sitting on plane with gravity. // Contact angle with plane can be varied. PARAMETER angle = 90 // interior angle between plane and surface, degrees gravity_constant 0 // start with gravity off #define WALLT (-cos(angle*pi/180)) // virtual tension of facet on plane constraint 1 /* the table top */ formula: x3 = 0 energy: // for contact angle e1: -(WALLT*y) e2: 0 e3: 0 vertices 1 0.0 0.0 0.0 constraint 1 /* 4 vertices on plane */ 2 1.0 0.0 0.0 constraint 1 3 1.0 1.0 0.0 constraint 1 4 0.0 1.0 0.0 constraint 1 5 0.0 0.0 1.0 6 1.0 0.0 1.0 7 1.0 1.0 1.0 8 0.0 1.0 1.0 9 2.0 2.0 0.0 fixed /* for table top */ 10 2.0 -1.0 0.0 fixed 11 -1.0 -1.0 0.0 fixed 12 -1.0 2.0 0.0 fixed edges /* given by endpoints and attribute */ 1 1 2 constraint 1 /* 4 edges on plane */ 2 2 3 constraint 1 3 3 4 constraint 1 4 4 1 constraint 1 5 5 6 6 6 7 7 7 8 8 8 5 9 1 5 10 2 6 11 3 7 12 4 8 13 9 10 fixed /* for table top */ 14 10 11 fixed 15 11 12 fixed 16 12 9 fixed faces /* given by oriented edge loop */ 1 1 10 -5 -9 2 2 11 -6 -10 3 3 12 -7 -11 4 4 9 -8 -12 5 5 6 7 8 7 13 14 15 16 density 0 fixed /* table top for display */ bodies /* one body, defined by its oriented faces */ 1 1 2 3 4 5 volume 1 density 1 read re := refine edges where on_constraint 1The mound itself was basically copied from
cube.fe, but
with face 6 deleted. The reason for this is that face 6 is
not needed, and would actually get in the way. It is not
needed for the volume calculation since it would always be
at z = 0 and thus not contribute to the surface integral
for volume.
The bottom edges of the side faces are constrained to lie in
the plane z = 0, so face 6 is not needed to keep them from
catastrophically shrivelling up. We could have handled the
contact angle by including face 6 with a surface tension equal
to the interface energy density between the liquid and
surface, but that can cause problems if the edges around face
6 try to migrate inward. After refinement a couple of times,
interior vertices of the original
face 6 have no forces acting on them, so
they don't move. Hence it would be tough for face 6 to shrink
when its outer vertices ran up against its inner vertices.
The tabletop face, face 7, is entirely extraneous to the
calculations. Its only purpose is to make a nice display.
You could remove it and all its vertices and edges without
affecting the shape of the mound. It's constraint 1 that is
the tabletop as far as the mound is concerned. To see what
happens with the bottom face present, load
moundB.fe and do "run".
Now run Evolver on mound.fe.
The command "re" defined at the
end of the datafile is good to use first in order to refine
some edges that need it. Refine and iterate a while.
You should get a nice mound. It's not a hemisphere, since
gravity is on by default with G = 1. If you use the
G
command to set "G 0" and iterate a while, you get a
hemisphere. Try changing the
contact angle, to 45 degrees (with the
command "angle := 45"}
or 135 degrees for example.
You can also play with gravity. Set "G 10" to get a
flattened drop, or "G -5" to get a drop hanging from the
ceiling. "G -10" will
cause the drop to try to break loose,
but it can't, since its vertices are still constrained.